Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
Symbol
Value
I
1
V
5
X
10
L
50
C
100
D
500
M
1000
For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as, XII, which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
I can be placed before V (5) and X (10) to make 4 and 9.
Example 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 Example 1: Input: "III" Output: 3 Example 2: Input: "IV" Output: 4 Example 3: Input: "IX" Output: 9 Example 4: Input: "LVIII" Output: 58 Explanation: L = 50, V= 5, III = 3. Example 5: Input: "MCMXCIV" Output: 1994 Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
JAVA题解 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 package algorithm;import java.util.HashMap;import java.util.Map;public class Leetcode13 { public static int romanToInt (String s) { int [] moneys = new int []{1000 , 900 , 500 , 400 , 100 , 90 , 50 , 40 , 10 , 9 , 5 , 4 , 1 }; String[] moneyToStr = new String []{"M" , "CM" , "D" , "CD" , "C" , "XC" , "L" , "XL" , "X" , "IX" , "V" , "IV" , "I" }; char [] chars = s.toCharArray(); int result = 0 ; int tempJ = 0 ; for (int i = 0 ; i < chars.length; ) { for (int j = tempJ; j < moneyToStr.length; ) { if (new String (new char []{chars[i]}).equals(moneyToStr[j])) { result += moneys[j]; i++; tempJ = j; break ; } else if (i + 1 < chars.length && new String (new char []{chars[i], chars[i + 1 ]}).equals(moneyToStr[j])) { result += moneys[j]; i += 2 ; tempJ = j + 1 ; break ; } else { j++; } } } return result; } public static int romanToInt1 (String s) { Map<String, Integer> map = new HashMap <>(); map.put("I" , 1 ); map.put("IV" , 4 ); map.put("V" , 5 ); map.put("IX" , 9 ); map.put("X" , 10 ); map.put("XL" , 40 ); map.put("L" , 50 ); map.put("XC" , 90 ); map.put("C" , 100 ); map.put("CD" , 400 ); map.put("D" , 500 ); map.put("CM" , 900 ); map.put("M" , 1000 ); int ans = 0 ; for (int i = 0 ;i < s.length();) { if (i + 1 < s.length() && map.containsKey(s.substring(i, i+2 ))) { ans += map.get(s.substring(i, i+2 )); i += 2 ; } else { ans += map.get(s.substring(i, i+1 )); i ++; } } return ans; } public static void main (String[] args) { System.out.println(romanToInt("XIX" )); } }
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string “”.
Example 1 2 3 4 5 6 7 8 9 10 11 12 13 Example 1: Input: ["flower","flow","flight"] Output: "fl" Example 2: Input: ["dog","racecar","car"] Output: "" Explanation: There is no common prefix among the input strings. Note: All given inputs are in lowercase letters a-z.
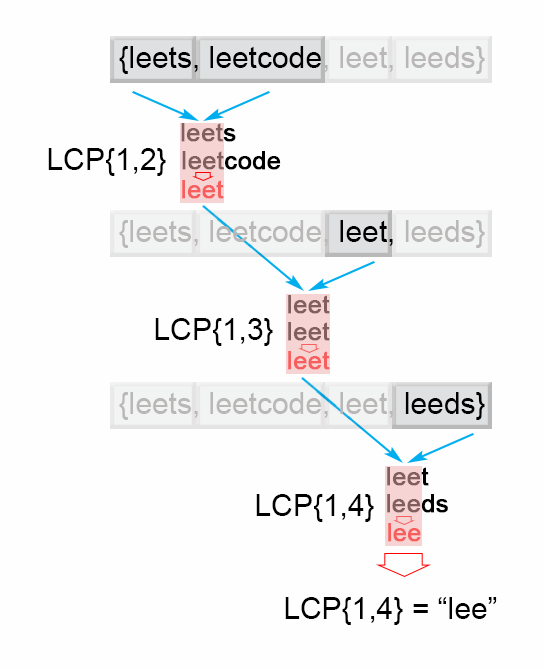
JAVA题解 水平扫描
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 package algorithm;public class Leetcode14 { public static String longestCommonPrefix (String[] strs) { if (strs.length == 0 ) { return "" ; } if (strs.length == 1 ) { return strs[0 ]; } int i = 0 ; String pre = "" ; for (; i < strs[0 ].length(); i++) { pre = strs[0 ].substring(0 , i + 1 ); int j = 1 ; boolean end = false ; for (; j < strs.length; j++) { if (!strs[j].startsWith(pre)) { break ; } if (pre.length() == strs[j].length()) { end = true ; } } if (j == strs.length && !end) { continue ; } else if (j != strs.length) { if (pre.length() > 1 ) { return pre.substring(0 , pre.length() - 1 ); } else { return "" ; } } else { return pre; } } return pre; } public static String longestCommonPrefix1 (String[] strs) { if (strs.length == 0 ) return "" ; String prefix = strs[0 ]; for (int i = 1 ; i < strs.length; i++) while (strs[i].indexOf(prefix) != 0 ) { prefix = prefix.substring(0 , prefix.length() - 1 ); if (prefix.isEmpty()) return "" ; } return prefix; } public static void main (String[] args) { System.out.println(longestCommonPrefix1(new String []{"flower" ,"fl" ,"flight" })); } public static String longestCommonPrefix2 (String[] strs) { if (strs == null || strs.length == 0 ) return "" ; for (int i = 0 ; i < strs[0 ].length() ; i++){ char c = strs[0 ].charAt(i); for (int j = 1 ; j < strs.length; j ++) { if (i == strs[j].length() || strs[j].charAt(i) != c) return strs[0 ].substring(0 , i); } } return strs[0 ]; } }
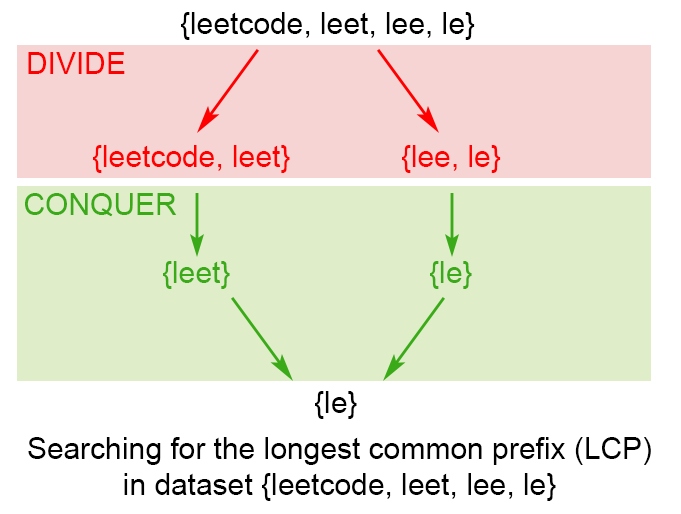
分治算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public String longestCommonPrefix (String[] strs) { if (strs == null || strs.length == 0 ) return "" ; return longestCommonPrefix(strs, 0 , strs.length - 1 ); } private String longestCommonPrefix (String[] strs, int l, int r) { if (l == r) { return strs[l]; } else { int mid = (l + r)/2 ; String lcpLeft = longestCommonPrefix(strs, l , mid); String lcpRight = longestCommonPrefix(strs, mid + 1 ,r); return commonPrefix(lcpLeft, lcpRight); } } String commonPrefix (String left,String right) { int min = Math.min(left.length(), right.length()); for (int i = 0 ; i < min; i++) { if ( left.charAt(i) != right.charAt(i) ) return left.substring(0 , i); } return left.substring(0 , min); }
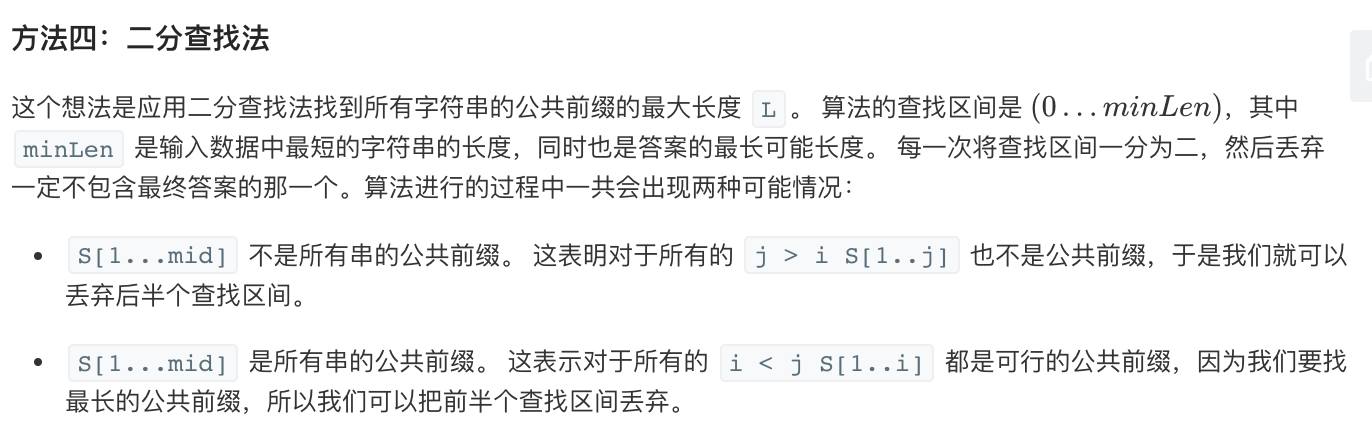
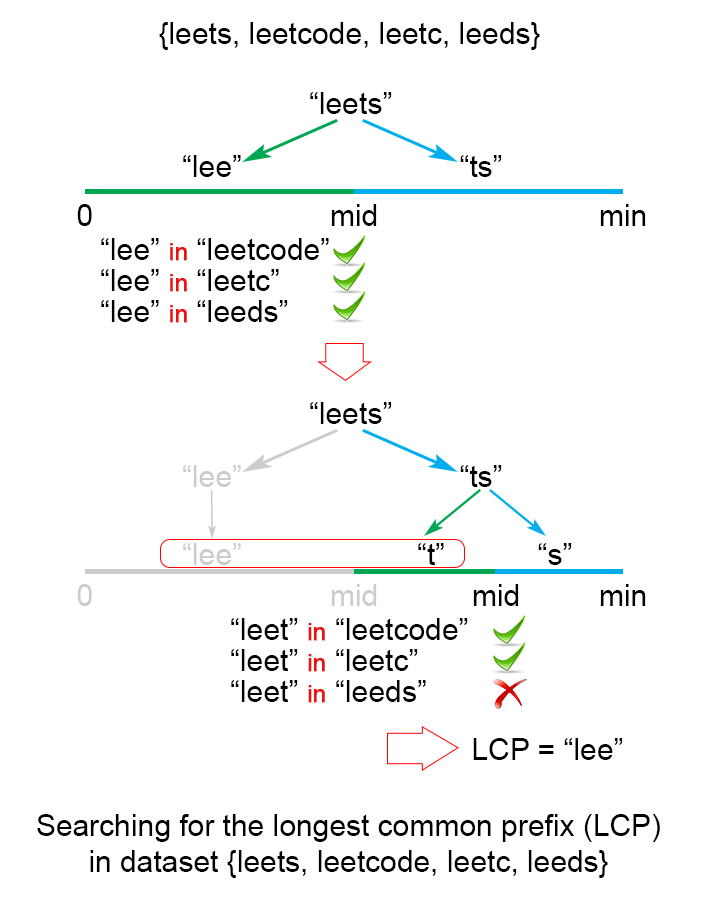
二分查找法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public String longestCommonPrefix (String[] strs) { if (strs == null || strs.length == 0 ) return "" ; int minLen = Integer.MAX_VALUE; for (String str : strs) minLen = Math.min(minLen, str.length()); int low = 1 ; int high = minLen; while (low <= high) { int middle = (low + high) / 2 ; if (isCommonPrefix(strs, middle)) low = middle + 1 ; else high = middle - 1 ; } return strs[0 ].substring(0 , (low + high) / 2 ); } private boolean isCommonPrefix (String[] strs, int len) { String str1 = strs[0 ].substring(0 ,len); for (int i = 1 ; i < strs.length; i++) if (!strs[i].startsWith(str1)) return false ; return true ; }
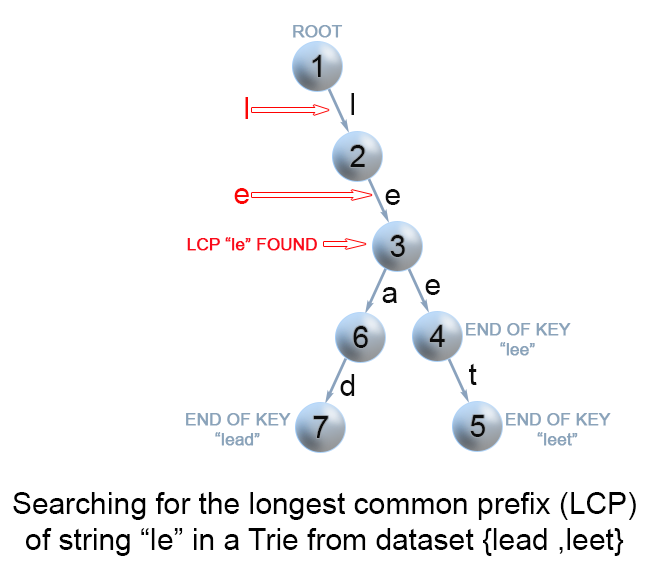
字典树 给定一些键值字符串 S = [S 1 ,S 2 …S n ],我们要找到字符串 q 与 S 的最长公共前缀。 这样的查询操作可能会非常频繁。
我们可以通过将所有的键值 S 存储到一颗字典树中来优化最长公共前缀查询操作。 如果你想学习更多关于字典树的内容,可以从 208. 实现 Trie (前缀树) 开始。在字典树中,从根向下的每一个节点都代表一些键值的公共前缀。 但是我们需要找到字符串q 和所有键值字符串的最长公共前缀。 这意味着我们需要从根找到一条最深的路径,满足以下条件:
这是所查询的字符串 q 的一个前缀
路径上的每一个节点都有且仅有一个孩子。 否则,找到的路径就不是所有字符串的公共前缀
路径不包含被标记成某一个键值字符串结尾的节点。 因为最长公共前缀不可能比某个字符串本身长
算法
最后的问题就是如何找到字典树中满足上述所有要求的最深节点。 最有效的方法就是建立一颗包含字符串[S 1 …S n ] 的字典树。 然后在这颗树中匹配 q 的前缀。 我们从根节点遍历这颗字典树,直到因为不能满足某个条件而不能再遍历为止。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 public String longestCommonPrefix (String q, String[] strs) { if (strs == null || strs.length == 0 ) return "" ; if (strs.length == 1 ) return strs[0 ]; Trie trie = new Trie (); for (int i = 1 ; i < strs.length ; i++) { trie.insert(strs[i]); } return trie.searchLongestPrefix(q); } class TrieNode { private TrieNode[] links; private final int R = 26 ; private boolean isEnd; private int size; public void put (char ch, TrieNode node) { links[ch -'a' ] = node; size++; } public int getLinks () { return size; } } public class Trie { private TrieNode root; public Trie () { root = new TrieNode (); } private String searchLongestPrefix (String word) { TrieNode node = root; StringBuilder prefix = new StringBuilder (); for (int i = 0 ; i < word.length(); i++) { char curLetter = word.charAt(i); if (node.containsKey(curLetter) && (node.getLinks() == 1 ) && (!node.isEnd())) { prefix.append(curLetter); node = node.get(curLetter); } else return prefix.toString(); } return prefix.toString(); } }