11. Container With Most Water
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
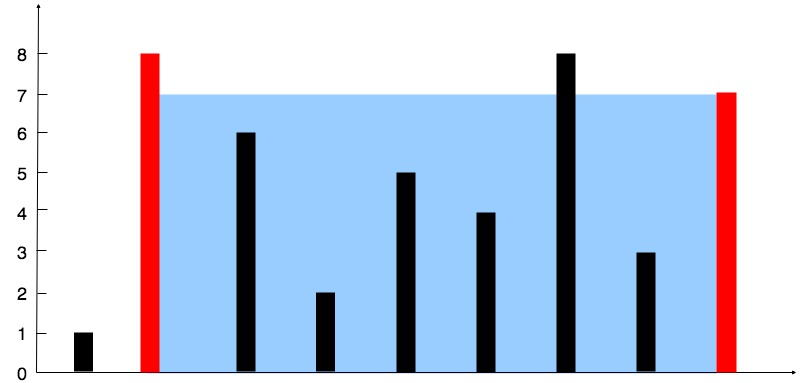
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example
1 | Example: |
JAVA题解
1 | package algorithm; |
12. Integer to Roman
Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
Symbol Value
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
For example, two is written as II in Roman numeral, just two one’s added together. Twelve is written as, XII, which is simply X + II. The number twenty seven is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
I can be placed before V (5) and X (10) to make 4 and 9.
X can be placed before L (50) and C (100) to make 40 and 90.
C can be placed before D (500) and M (1000) to make 400 and 900.
Given an integer, convert it to a roman numeral. Input is guaranteed to be within the range from 1 to 3999.
Example
1 | Example 1: |
JAVA题解
1 | package algorithm; |