Hash碰撞
Hash函数就是将任意长度的输入转化成固定长度的输出的一类函数。
比如说我的输入是任意一个自然数(0,1,2,3…),而我要求经过一个函数后我的输出的数的范围要在0-9这样一个范围之间。
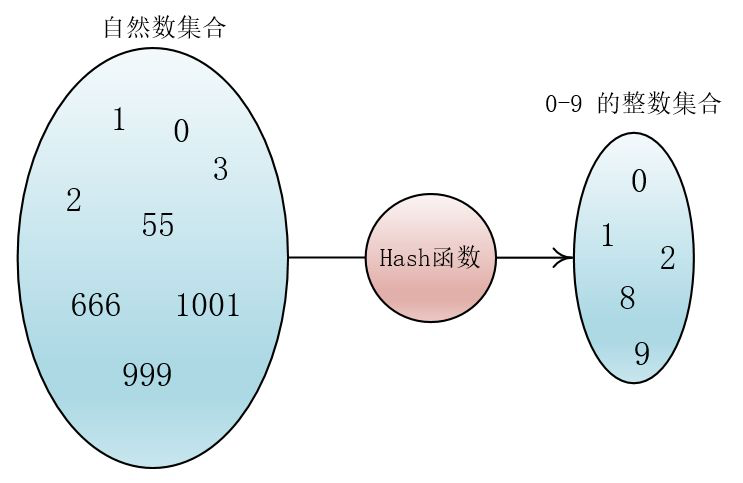
很容易想到,我们可以使用Hash函数:
Hash(key) = key % 10
其中key就是输入
在哈希表(散列表)里,Hash函数的作用就是将关键字Key转化为一个固定长度数组的下标,以便存取键值对<Key,Value>
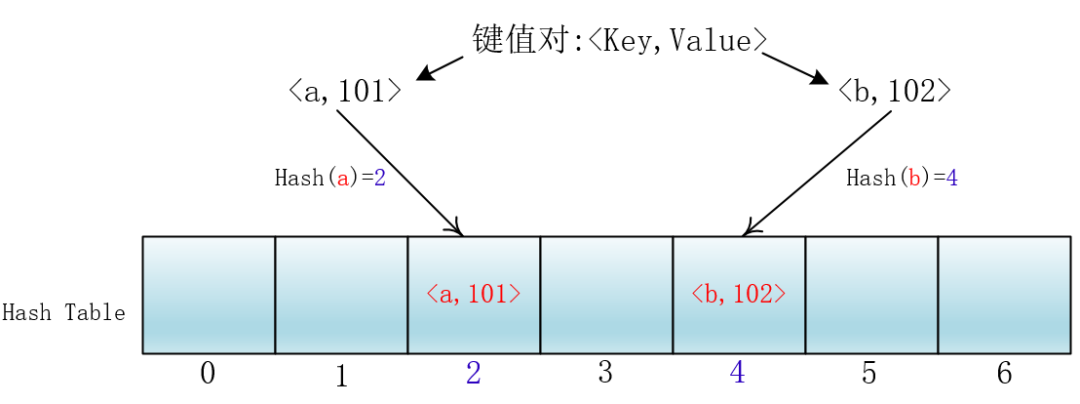
当多个键(key)经过Hash函数处理后落在了同一个位置时怎么办呢?
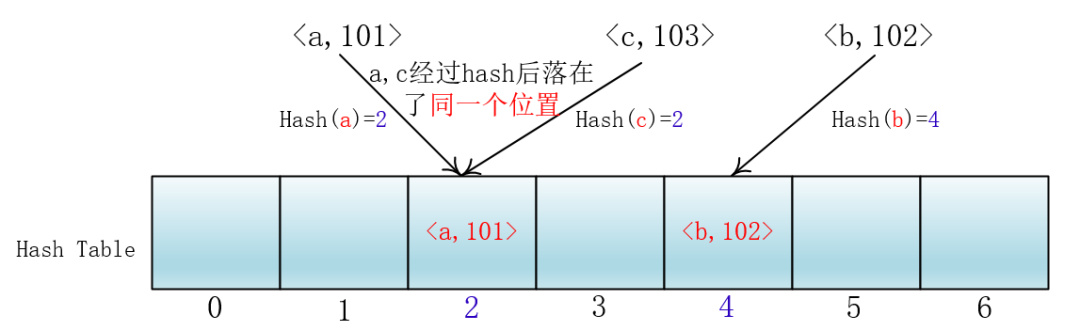
此时使用链地址法可看:神速Hash
链地址法
用链表,来一个元素加一个,让这个位置存储一个指针,指向一个链表,让所有相同位置的元素都放在这个链表中
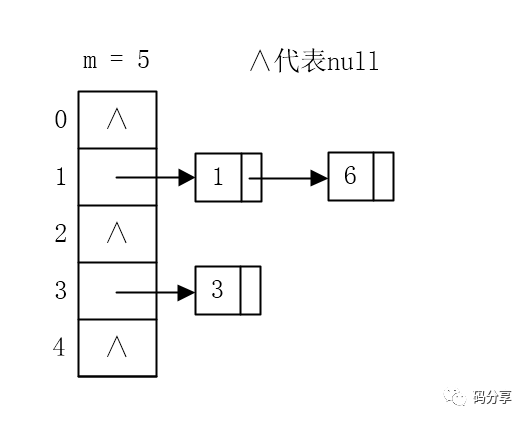
在存储的时候,如果多个元素被Hash到同一位置,那么就加入到该位置所指向的链表中,如果该位置没有元素,则为null(指向空)。
此图中6先放进去了,因为这个插入链表的时候要采用‘头插’的方式,也就是插入链表的最前面(图中里数组最近的元素)。
因为经常发生这样的事情:新加入的元素很可能被再次访问到,所以放到头的话,如果查找就不用再遍历链表了。
rehash
Hash函数设计的非常好,能够将元素均匀Hash(散列)开来,但是当我们实际存入的值越来越多的时候,这个链表也势必越来越长,那当我们进行查找的时候,势必就会遍历链表,是否效率也就越来越慢?
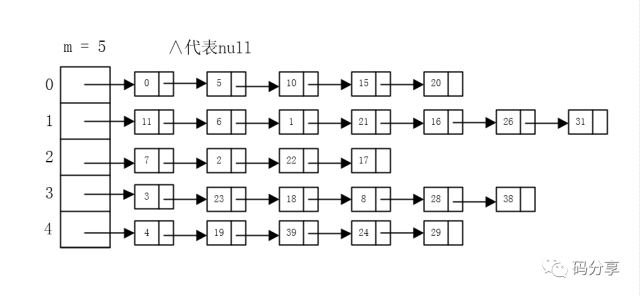
这样的话,随着链表的不断增长,查询某一个元素的时间也就增加了,如果链表长度远远大于数组长度,不就和用链表存储一样了吗?
对,现在只能扩大数组的长度大约为原来的两倍
然后选取一个相关的新的Hash函数(比如之前使用 key % m,现在只改变一下m的值)
将旧Hash表中所有的元素通过新的Hash函数计算出新的Hash值,并将其插入到新表中(仍然使用链表),这就叫rehash
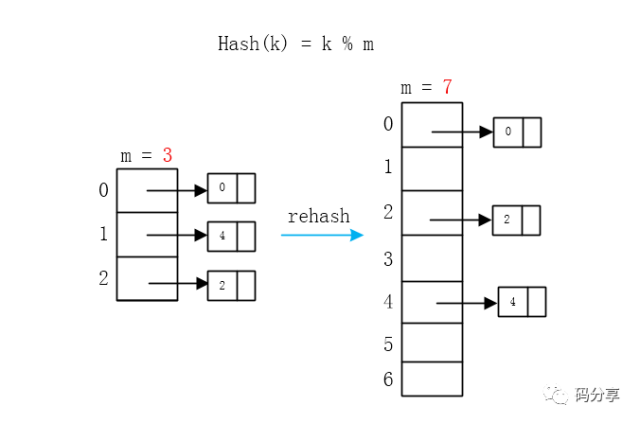
这里的数组就扩大了近两倍,由于要大小要选素数,那就选原数组大小两倍后的第一个素数7,旧Hash表和新Hash表采用了不同的Hash函数,但相关,只是m的取值变了。
什么时候开始rehash?
装载因子 α
我们可以定义这样一个变量 α = 所有元素个数/数组的大小,我们叫它装载因子吧,它代表着我们的Hash表(也就是数组)的装满程度,在这里也代表链表的平均长度。
比如说,我们的数组大小为 5 ,我们给里面存入 3个元素,那么 α = 3/5 =0.6, 这个Hash表装满程度为60%,平均每条链有0.6个元素,当然 α 也可以等于和大于 1。
这个装载因子代表了Hash表的装满程度,这里也可以代表链表的平均长度,那么也就可以代表查询时的时间长短了
基于此,我们为了不让查询时间长,也就是查询性能低,我们可以设置一个临界 α 值,当随着存入元素导致 α 大于这个临界 α 值的时候
我们可以通过rehash来调整当前的 α 值,使之低于我们设定的 临界 α 值,从而使我们的查询性能保持在较好的范围之内
比如说,我们设定 临界 α = 0.7,对于一个Hash表大小为5的Hash表而言
当存入存入第四个元素的时候,α 就超出了临界 α 值,我们可以将数组长度变为11进行rehash(因为11是原表两倍后的第一个素数),使得装载因子 α 小于 0.7
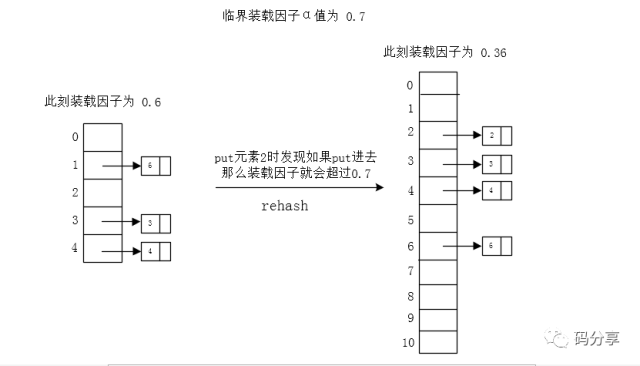
通过rehash我们可以使得装载因子在一定范围内,那我们的查询性能也就得到了保证了
那这个 临界的 α 值应该选择多大呢?
这个 临界 α 如果选的小了,那数组的空间利用率就会太低,就比如说数组大小为100,α = 0.01,那装满程度为1%,99%还没有被利用
如果 α 太大了,那冲突就会很多,比如说 数组大小为 5,α = 10, 那平均每条链有10个元素,装满程度为1000%
即使Hash函数设计的合理,基本上每次存放元素的时候就会冲突,所以鉴于两者之间我觉得 0.6 - 0.9 之间是一个不错的选择,不妨选0.75。
开放地址法
所谓开放地址法就是发生冲突时在散列表(也就是数组里)里去寻找合适的位置存取对应的元素。
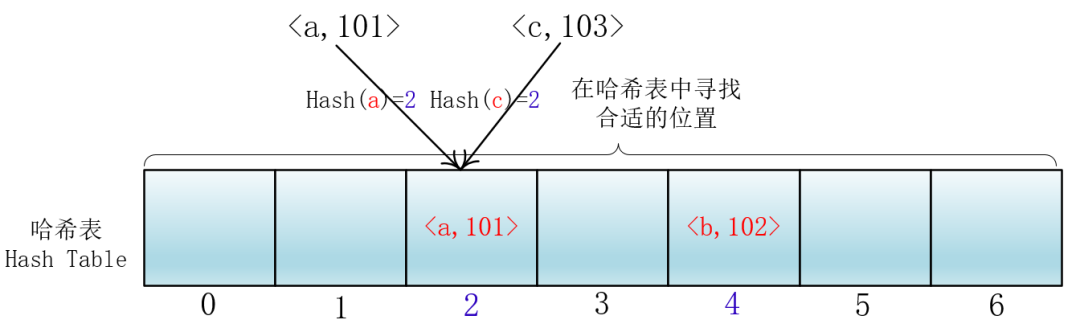
合适的位置该怎么找呢?
线性探测法
最容易想到的就是当前位置冲突了,那我就去找相邻的下一个位置。
就拿放入元素举例吧,当你放入<a,101>到下标为2的位置后,另一个<c,103>键值对也落入了这个位置,那么它就向后依次加一寻找合适的位置,然后把<c,103>放入进去。
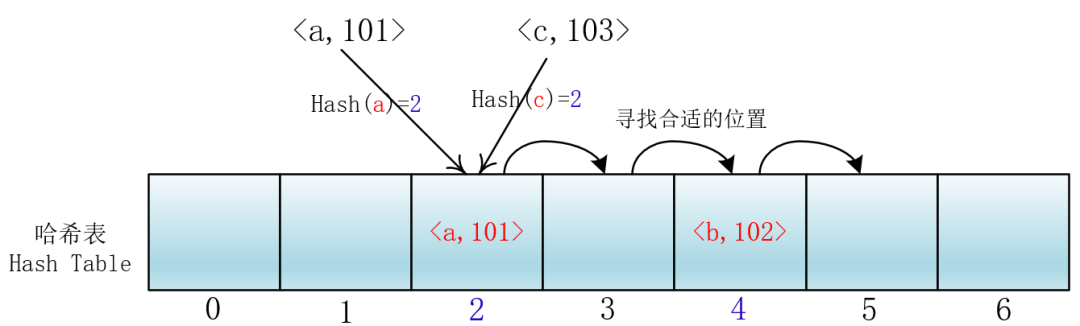
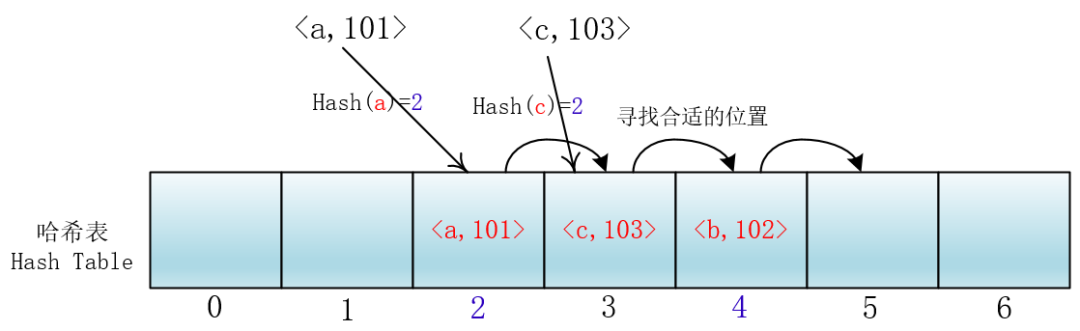
我们把这种方法称作线性探测法,我们可以将Hash以及寻找位置的过程抽象成一个函数:
hash(key) = (hash1(key) + i) % 7,i=0,1,2,...6
所以关键字要进行查找或者插入,首先看(hash1(key)+0)%7 位置是自己最终的位置吗?如果有冲突,就探测(查看)下一个位置:(hash1(key)+1)%7。依次进行
所谓探测,就是在插入的时候检查哪个位置可以插入,或者查找时查找哪个位置是要查找的键值对,本质就是探寻这个键值对最终的位置。
但是这样会有一个问题,就是随着键值对的增多,会在哈希表里形成连续的键值对
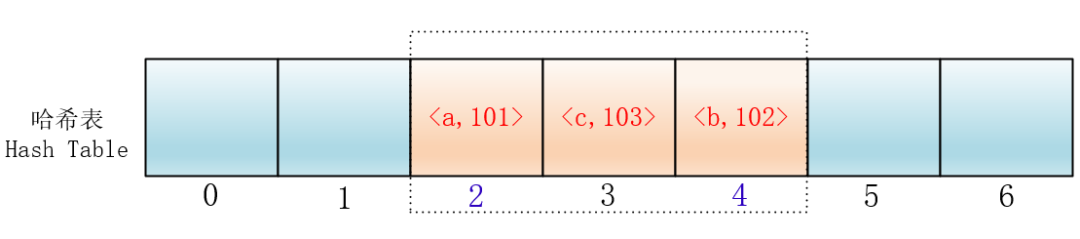
这样的话,当插入元素时,任意一个落入这个区间的元素都要一直探测到区间末尾,并且最终将自己加入到这个区间内。这样就会导致落在区间内的关键字Key要进行多次探测才能找到合适的位置,并且还会继续增大这个连续区间,使探测时间变得更长,这样的现象被称为“一次聚集(primary clustering)”
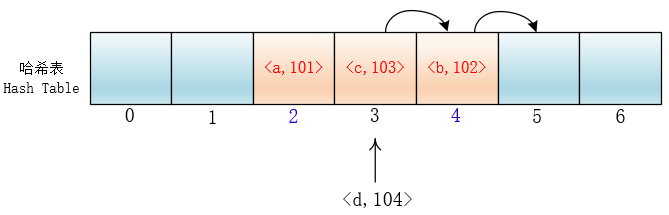

平方探测法
我们可以在探测时不一个挨着一个地向后探测,我们可以跳跃着探测,这样就避免了一次聚集。
其实我们可以让它按照 i^2 的规律来跳跃探测
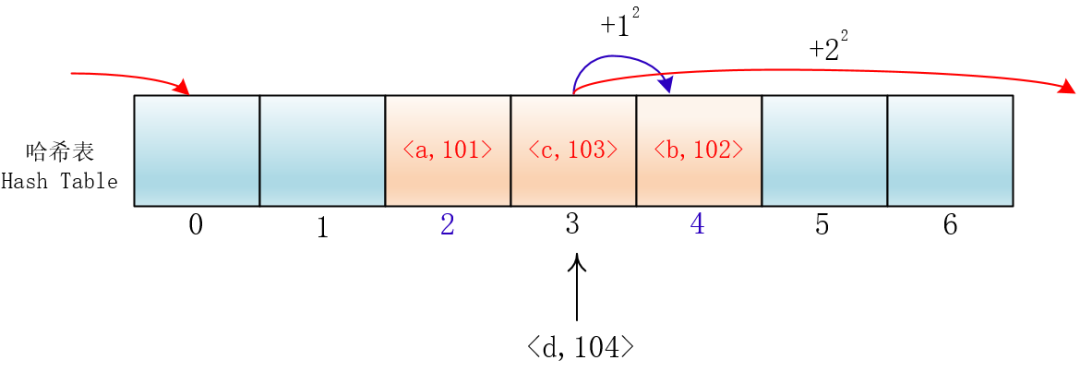
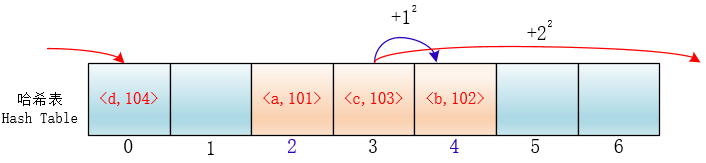
这样的话,元素就不会聚集在某一块区域了,我们把这种方法称为平方探测法
同样我们可以抽象成下面的函数:
hash(key) = (hash1(key) + i^2) % 7,i=0,1,2,...6
其实可以扩展到更一般的形式:
hash(key) = (hash1(key) +c1i+c2 i^2) % 7,i=0,1,2,...6
虽然平方探测法解决了线性探测法的一次聚集,但是它也有一个小问题,就是关键字key散列到同一位置后探测时的路径是一样的。
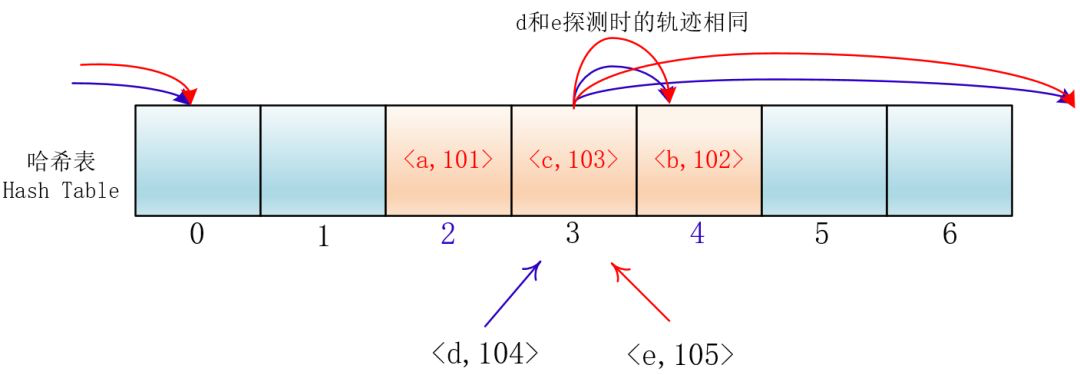
这样对于许多落在同一位置的关键字而言,越是后面插入的元素,探测的时间就越长。
这种现象被称作“二次聚集(secondary clustering)”,其实这个在线性探测法里也有。
这种现象出现的原因是由于对于落在同一个位置的关键字我们采取了一个依赖 i 的函数(i或者i^2)来进行探测,它不会因为关键字的不同或其他因素而改变探测的路径。那么我们是不是可以让探测的方法依赖于关键字呢?
双散列
答案是可以的,我们可以再弄另外一个Hash函数,对落在同一个位置的关键字进行再次的Hash,探测的时候就用依赖这个Hash值去探测,比如我们可以使用下面的函数:
hash(key) = (hash1(key) +hash2(key)*i) % 7,i=0,1,2,...6
经过hash1的散列后,会定位到某一个地址,如果这个地址冲突,那么就按照1hash2(key)、2hash2(key)… 的偏移去探测合适的位置。
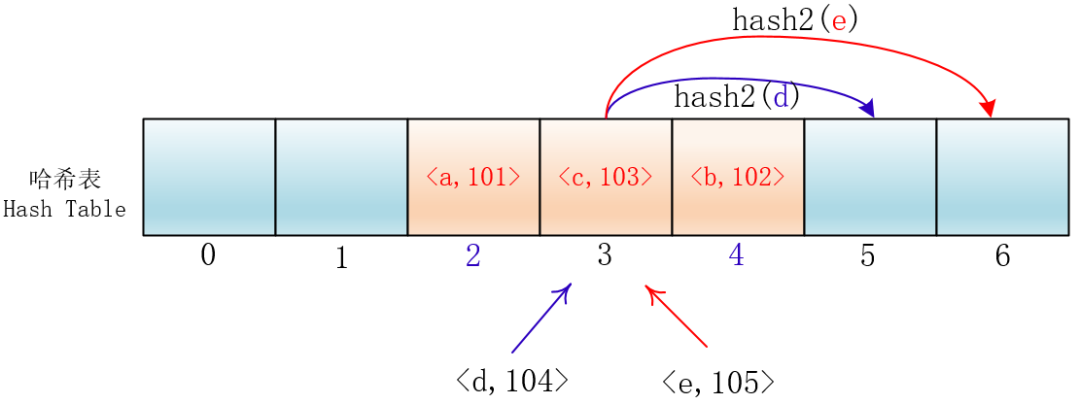
由于Hash2函数不同于Hash1,所以两个不同的关键字Hash1值和Hash2值同时相同的概率就会变得非常低。
这样就避免了二次聚集,但同时也付出了计算另一个散列函数Hash2的代价。
如果hash2(key)=0,那探测不就一直在原地不动,失效了吗?
所以hash2函数在选择的时候要避免这种情况。
参考文章:
参考链接1